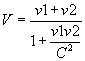Questions de vitesse, de marées et de ciel noir

Orion et ses géantes

1. La vitesse de la lumière est de 300 000 KM/S . Rien ne va plus vite.

      Or, chacun sait que 2 trains qui se croisent, donne l'impression pour ceux qui sont à l'intérieur, que la vitesse du croisement résulte de l'addition des 2 vitesses. On démontre en mécanique que la résultante de 2 vitesses parallèles est égale à leur somme algébrique.

      Si nos 2 trains roulent à la vitesse de la lumière, chacun est convaincu que la même règle s'applique. Et pourtant, pour les gens à l'intérieur du train, la vitesse est de 300 000 Km/s.  Pourquoi ?...

       Tout simplement, nous avons l'habitude d' appliquer une équation incomplète, celle de la vitesse. En effet, c'est l'expérience de Michelson, en 1881, qui battit en brèche cette idée reçue, sur l'addition des vitesses. Il démontra d' une façon éclatante que la vitesse de la lumière est invariable quelle que soit la direction. Le résultat fut tellement surprenant que l'expérience fut reprise plusieurs fois par d'autres scientifiques avec des appareillages différents et extrêmement précis. Le résultat fut toujours le même.

         La raison de cette échec vient de l'emploi d'une équation incomplète qui oublie que la somme des   vitesses, v1 et v2, subit une contraction d'autant plus importante que l'on approche celle de la lumière, C².

        La vraie formule est celle de Lorentz:

   Aux vitesses très inférieures de celle de la lumière, la somme est celle connue de tous car le dénominateur est voisin de  1

retour à étoile

2. Pourquoi il y a-t-il 2 marées par jour? Suivre le lien pour la réponse.

   Si vous croyez que cette question est banale, pensez-y quand même, avant de lire la suite. De nombreuses personnalités ont mis des siècles pour en trouver la réponse.

   Dire que le ciel nocturne est noir semble être une banalité. Pourtant, dans un univers rempli d'étoiles, un ciel noir est impossible. Toute ligne de visée finit par rencontrer une étoile. Ainsi le ciel devrait avoir une brillance égale à la moyenne des brillances des étoiles.

    La connaissance de la thermodynamique (physique de la matière et de l'énergie) par les scientifiques étant bien acquise, ils réalisèrent que le ciel noir est en contradiction avec leur savoir.

    Au début du 17e siècle, Kepler avait remarqué ce paradoxe, puis en 1720, Edmond Halley se posa la même question. Par la suite d'autres personnages s'en intéressèrent, comme le Suisse Jean Philippe Loys de Chéseaux en 1743, qui lui, trouva une explication. Mais c'est l'Allemand Heinrich Olbers qui lui donna son nom en 1826: le paradoxe d'Olbers.

    Tout d'abord, ils pensèrent que de grandes quantités de poussières interstellaires interceptaient la lumière. Ce n'était pas la bonne réponse. C'est alors que l'on commença à parler de l'expansion de l'univers et de vitesse finie de la lumière. En effet, celle-ci impose un horizon au domaine visible et il y a trop peu d'étoiles dans le volume observable pour que leur éclat soit gênant.

    En 1848, Edgar Poe trouva les étoiles pas assez vieilles pour nous éblouir, dans sa pièce :" Eureka, a prox poem". Mais elle n'eut pas de succès et sa remarque sombra dans l'oubli.   A l'aube du 20e siècle, il en fut de même pour William Thomson qui estima, dans un calcul resté célèbre, qu'il était inutile de faire appel à autre chose qu'à l'âge des étoiles. Ce n'est que dans les années 1870, qu'Edward Harrison reconnut la justesse de Thomson et d'Edgar Poe. Il déclara que le nombre d'étoiles dans le volume qui nous est délimité par la vitesse de la lumière, est trop faible pour que le ciel soit lumineux. La lumière ne va pas assez vite et l'univers est très âgé.

retour à astéroïdes  sommaire    formulaire