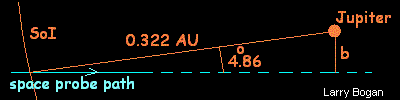Assistance gravitationnelle

Sphère d'influence

par Larry Bogan

  Une sonde qui s'approche d'une planète peut se servir du champ gravitationnel de la planète pour accroître ou diminuer sa vitesse. Lorsqu'il y a gain de vitesse on parle de fronde gravitationnelle ou effet catapulte (slingshot). 

Retour

9. Changement de référentiel

 

Le passage de la sonde à l'intérieur de la sphère d'influence de Jupiter (orbite d'insertion)  dépend de la vitesse et de la position de la sonde à l'entrée de la sphère. La vitesse dépend  de l'orbite du vaisseau spatial et la vitesse de Jupiter. Le schéma ci-contre représente la traduction dans le référentiel de Jupiter où la vitesse de la sonde est de 7,91 km/s. C'est supérieur à la vitesse d'évasion de Jupiter et le vaisseau spatial passera rapidement au-dessus de la planète en quittant  la sphère d'influence à la même vitesse.

http://www.go.ednet.ns.ca/~larry/orbits/gravasst/V_wrt_j.gif

10. Position relative

 

Vitesse d'évasion: vévasion = [2MJG/r]1/2 MJG = 1,267x108 km (km/s)2 = 0,847 AU(km/s)2 r = 0,322 UA (rayon de la sphère d'influence) vévasion = [2x0,847 AU(km/s)2/0,322 AU]1/2 = 2,29 km/s

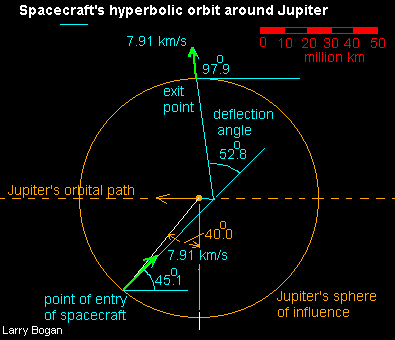
   L'autre aspect du passage à proximité de Jupiter dépend de la position relative de la sonde vis à vis de la planète. Cela dépend du chronomètre.  La phase de la vitesse est de - 45°, le vaisseau spatial pénètrera sur l'orbite d'insertion vers l'avant de cet angle, il sera alors attiré directement par la planète. Cette position est ajustée selon la précision de l'heure d'arrivée. Pour un angle de 40° , la sonde passe à 4,8° de la planète. Le paramètre d'impact qui lui correspond est déterminé par la géométrie et est égal à 0,273 UA ou 4,085 millions de km. 

 

b = 0,322UA sin(44,9° - 40°) = 0,0273 UA

 http://www.go.ednet.ns.ca/~larry/orbits/gravasst/b_calc.gif

11. Trajectoire hyperbolique de la nouvelle orbite

 

L'angle de déflexion peut maintenant être déterminé en utilisant:  cotg q = b v2/(GMJ). q = 26,4o et la déflexion totale = 2q = 52,8o   Puisque l'orbite de Jupiter est symétrique, l'angle de la sonde en quittant l'orbite d'insertion est déterminé. Comme écrit ci-dessus, la vitesse de sortie est la même que celle d'entrée. C'est tout ce qui est nécessaire pour déterminer la nouvelle orbite. Il est intéressant de suivre le trajet de la sonde à proximité de Jupiter. Les paramètres de l'orbite hyperbolique sont: e = 2, 25 a = 0,0148 UA = 2,21 millions de km rp = 2,76 millions de km

 http://www.go.ednet.ns.ca/~larry/orbits/gravasst/sc_orb_j.gif

  Notez que le vaisseau navigue bien en dehors des orbites des satellites galiléens. C'est différent du trajet des sondes Voyager 1 et Voyager 2.

12. Nouvelle orbite

 http://www.go.ednet.ns.ca/~larry/orbits/gravasst/V_wrtsun.gif
     L'étape finale pour décrire le trajet de la sonde sera de déterminer son orbite après avoir quitté la sphère d'influence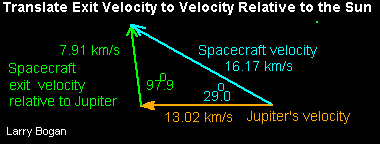 de Jupiter. La vitesse relative par rapport à celle de Jupiter est la même que celle qu'elle avait en entrant dans la sphère d'influence, mais avec un angle de 53°. Quand cette vitesse est ramenée par rapport au Soleil, la vitesse de Jupiter s'ajoute (dans le sens de la progression sur l'orbite) à la composante de vitesse du vaisseau spatial. Comme nous pouvons le constater dans le schéma de droite, la vitesse du vaisseau spatial s'est accrue  par rapport au soleil. Elle est passée à 16,17 km/s contre 9,36 km/s avant sa rencontre avec Jupiter. Jupiter a servi de tremplin gravitationnel. L'énergie cinétique a été multipliée par 3. L'énergie de masse de l'orbite a elle-même changé de - 126,7 à - 39,8 (km/s)². Le fait que l'énergie de l'orbite est négative signifie toujours que l'orbite est elliptique et la sonde est encore liée au soleil. (Une orbite à énergie zéro est parabolique tandis qu'une orbite à énergie positive est hyperbolique toutes les deux  permettant au vaisseau de s'échapper de l'emprise du soleil).

13. Paramètres orbitaux de la nouvelle orbite
    
      La taille, la forme et l'orientation de la nouvelle orbite sont déterminées en utilisant les mêmes équations pour l'orbite elliptique. Les étapes seront les suivantes:

• Evaluer GM_Soleil = 887 UA (km/s)²
• Toute l'énergie de masse de l'orbite est constante, ainsi en évaluant l'énergie cinétique et l'énergie gravitationnelle en un point de l'orbite, nous avons la valeur: 
  v = 16,17 km/s et  r = 5,20 UA
  E = mv²/2 - GM_Soleilm/r
  E/m = - 39,8 (km/s)²
• L'énergie de masse du vaisseau spatial détermine le  ½ grand  axe de l'orbite:
  a = -1/2 *(GM_Soleil)/(E/m) = 11,16 UA
• Ceci fourni alors la vitesse orbitale:
  v_c = GM_Soleil/a = - 2E/m = 8,92 km/s
• La période orbitale est donnée par la 3e loi de Kepler:
  P = a^3/2 = 37,28 années
• La vitesse locale est déjà connue par la vitesse et la position de la sonde.
  Il faut exprimer la vitesse en UA/an plutôt qu'en km/s: 4.74 km/s = 1 UA/an
  A = r v_/2 où le segment vitesse v_ = 16,17km/s cos 29^o
  v_ = 14,15 km/s = 2,985 UA/an
  A = 7.765 (UA)²/an
• L'autre méthode de détermination de la vitesse locale nous donne l'excentricité de l'orbite:
  A = surface de l'ellipse/période = pa²(1 - e²)^1/2/P
  1 - e² = 0,5474 et e = 0,673
• Nous connaissons maintenant la taille et la forme de l'orbite et nous pouvons déterminer ses dimensions:
  r_p (distance au périhélie) = a (1 - e) = 3,64 AU
  r_a (distance à l'aphèlie)= a (1 + e) = 18,67 AU
  L'orbite dépasse celle de Saturne mais ne va pas tout à fait à celle d'Uranus
  L'orbite ne croise pas celle de Mars, mais pénètre dans la ceinture des astéroïdes.
• Le paramètre final est l'anomalie vraie, déterminé par l'angle de la sonde au périhélie de la nouvelle orbite.
  Il faut résoudre r = a (1 - e²)/(1 + e cos q) pour q
  cos q = [a (1 - e²)/r - 1]/e
  q = 75,1^o
• Le schéma ci-dessous montre la trajectoire de la nouvelle orbite par rapport à l'ancienne.

http://www.go.ednet.ns.ca/~larry/orbits/gravasst/All_orbs.gif

  Puisque le vaisseau spatial croisera l'orbite de Saturne, si la synchronisation était exacte, le vaisseau spatial pourrait obtenir une accélération de Saturne pour accroître son énergie afin de l'envoyer vers  Uranus, Neptune ou pour échapper probablement à l'attraction solaire.

14. Voyage vers Vénus
    

   Voici un problème qui vous permettra de calculer le trajet Terre-Vénus et la manière de lancer la sonde en orbite autour de l'étoile du berger.

    La destination étant plus proche du Soleil, c'est l'aphélie qui sera égal à 1 UA, tandis que le périhélie sera égal à 0,723 UA (distance Vénus - Soleil). Le ½ grand axe (a) de l'orbite sera alors égal à 0,862. 

    La période pour parcourir cette orbite, selon la 3e loi de Kepler, sera de: T (ans) = (a³)^½ = 0,8 an

    Puisque le trajet correspond à la moitié de l'ellipse, 

  D'après les paramètres orbitaux à l'aphélie: distance à l'aphélie r_a = a (1 + e); l'excentricité e devient (r_a/a)-1.

  Si l'on définit v_moyenne comme la vitesse moyenne sur orbite, nous pouvons écrire que la vitesse sur une orbite circulaire = Circonférence / temps de parcours = 2pa/T

    v_moyenne  = 2pa/T (1-e²)^-½

  La vitesse au lancement = V_périhélie =V_moyenne (1+e) et  V_aphélie =V_moyenne (1-e)

  La vitesse que doit avoir la sonde au départ est V_aphélie = 2pa/T (1-e²)^-½ . (1-e)

NB: Pour les planètes du Système solaire le facteur (1-e²)^-½ est voisin de 1 , sauf Mercure et Pluton qui ont des e dépassant 0,2.

  Déterminons les équations en utilisant les mètres et les secondes:

   ½ grand axe (a) = 1,28.10¹¹ m et T = 2,52.10⁷ s, sachant T correspond au temps total du parcours de l'orbite soit 0,8 an.

  Après avoir effectué, nous trouvons V_aphélie = 27,2 km/s.  Sachant que la Terre a une vitesse orbitale de 29,7 km/s, il faut ralentir la sonde de 29,7 - 27,2 = 2,5 km/s pour qu'elle tombe vers le Soleil. 

“Kepler - Orbites  - Assistance gravitationnelle” par Larry Bogan

http://www.go.ednet.ns.ca/~larry/orbits/gravasst/gravasst.html

http://www.go.ednet.ns.ca/~larry/orbits/orbits.html

http://www.go.ednet.ns.ca/~larry/orbits/ellipse.html

http://www.go.ednet.ns.ca/~larry/orbits/kepler.html

“Assistance gravitationnelle en mécanique céleste” par James A. Van Allen

http://www.dur.ac.uk/bob.johnson/SL/AJP00448.pdf

 “Simulation d'une sonde planétaire”  http://www.pma.caltech.edu/~physlab/ph21/21_2.pdf

“Trajectoires en assistance gravitationnelle” http://users.erols.com/richdoran/assist

Retour

  JavaScript DHTML Drop Down Menu By Milonic